Estimating causal effects using geo experiments
by JOUNI KERMAN, JON VAVER, and JIM KOEHLER
What does it take to estimate the impact of online exposure on user behavior? Consider, for example, an A/B experiment, where one or the other version (A or B) of a web page is shown at random to a user. The analysis could then proceed with comparing the probabilities of clicking on a certain link on the page shown. The version of the web page that has a significantly higher estimated probability of click (click-through rate, or CTR) would be deemed the more effective one.
Similarly, we could test the effectiveness of a search ad compared to showing only organic search results. Whenever a user types in a specific search query, the system makes a split-second decision of whether or not to show a particular ad next to the organic results. Click-through rates can then be compared to determine the relative effectiveness of the presence of ads.
Traffic experiments like the ones above can randomize queries, but they cannot randomize users. The same user may be shown the ad whenever they perform the same search the second time. Traffic experiments, therefore, don't allow us to determine the longer term effect of the ad on the behavior of users.
We could approximate users by cookies. However, one user may have several devices (desktop, laptop, tablet, smartphone), each with its own cookie space. Moreover, cookies get deleted and regenerated frequently. Cookie churn increases the chances that a user may end up receiving a mixture of both the active treatment and the control treatment.
Even if we were able to keep a record of all searches and ad clicks and associate them with online conversions, we would still not be able to observe any long-term behavior. A conversion might happen days after the ad was seen, perhaps at a regular brick-and-mortar store. This makes it difficult to attribute the effect of an online ad on offline purchases.
It is important that we can measure the effect of these offline conversions as well. How can we connect an event of purchase to the event of perceiving the ad if the purchase does not happen immediately? And, from the perspective of the experiment set-up, how can we ensure that a user whom we assigned to the control group won't ever see the ad during the experiment?
Another possibility is to run a panel study, an experiment with a recruited set of users who allow us to analyze their web and app usage, and their purchase behavior. Panel studies make it possible to measure user behavior along with the exposure to ads and other online elements. However, meaningful insights require a representative panel or an analysis that corrects for the sampling bias that may be present. In addition, panel studies are expensive. Wouldn't it be great if we didn't require individual data to estimate an aggregate effect? Let's take a look at larger groups of individuals whose aggregate behavior we can measure.
A geo experiment is an experiment where the experimental units are defined by geographic regions. Such regions are often referred to as Generalized Market Areas (GMAs) or simply geos. They are non-overlapping geo-targetable regions. This means it is possible to specify exactly in which geos an ad campaign will be served – and to observe the ad spend and the response metric at the geo level. We can then form treatment and control groups by randomizing a set of geos.
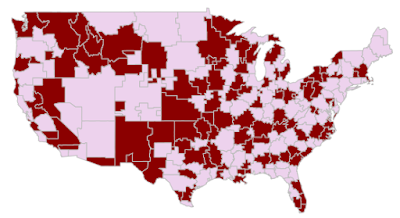
Consider, as an example, the partition of the United States into 210 GMAs defined by Nielsen Media. The regions were originally formed based on television viewing behavior of their residents, clustering together “exclusive geographic area of counties in which the home market television stations hold a dominance of total hours viewed.” These geos can be targeted individually in Google AdWords. Here is an example of a randomized assignment:
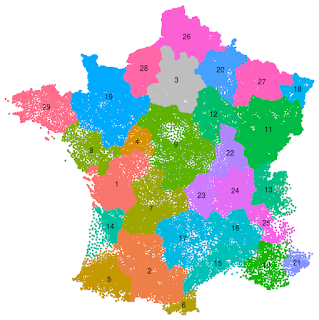
In contrast to the US, France doesn't currently have an analogous set of geos. So we created a set of geos using our own clustering algorithms. The figure below shows an example of a set of geos partitioning mainland France into 29 GMAs:
Suppose that users in control regions are served ads with a total spend intensity of $C$ dollars per week, while users in treatment regions are served ads with a cost of $T = C + A$ dollars per week ($A > 0$). The key assumption in geo experiments is that users in each region contribute to sales only in their respective region. This assumption allows us to estimate the effect of the ad spend on sales. What makes geo experiments so simple and powerful is that they allow us to capture the full effects of advertising, including offline sales and conversions over longer periods of time (e.g., days or weeks).
The quantity that we aim to estimate, in particular, is a specific type of return on investment where the investment is the cost of advertising. We often refer to this as the Return On Ad Spend (ROAS). Even more specifically, we are typically interested in the change in sales (or website visits, conversions, etc.) when we change the ad spend: the incremental ROAS, or iROAS. When response is expressed in terms of the same currency as the investment, iROAS is just a scalar. For example, an iROAS of 3 means that each extra dollar invested in advertising leads to 3 incremental dollars in revenue. Alternatively, when the response is the number of conversions, iROAS can be given in terms of number of conversions per additional unit of currency invested, say “1000 incremental conversions per 10,000 additional dollars spent.” In other words, iROAS is the slope of a curve of the response metric plotted against the underlying advertising spend.
During the test period (which is typically 3 to 5 weeks long), geos in the treatment group are targeted with modified advertising campaigns. We know that this modification, by design, causes an incremental effect on ad spend. What we don't know is whether it also causes an incremental effect in the response metric. It is worth noting that modified campaigns may cause the ad spend to increase (e.g., by adding keywords or increasing bids in the AdWords auction) or decrease (e.g., by turning campaigns off). Either way, we typically expect the response metric to be affected in the same direction as spend. As a result, the iROAS is typically positive.
After the test period finishes, the campaigns in the treatment group are reset to their original configurations. This doesn't always mean their causal effects will cease instantly. Incremental offline sales, for example, may well be delayed by days or even weeks. When studying delayed metrics, we may therefore want to include in the analysis data from an additional cool-down period to capture delayed effects.
Statistical power is traditionally given in terms of a probability function, but often a more intuitive way of describing power is by stating the expected precision of our estimates. We define this as the standard error of the estimate times the multiplier to obtain the bounds of a confidence interval. This could, for example, be stated as the “iROAS point estimate +/- 1.0 for a 95% confidence interval”. This is a quantity that is easily interpretable and summarizes nicely the statistical power of the experiment.
The expected precision of our inferences can be computed by simulating possible experimental outcomes. We also check that the false positive rate (i.e., the probability of obtaining a statistically significant result if the true iROAS is in fact zero) is acceptable, such as 5% or 10%. This power analysis is absolutely essential in the design phase as the amount of proposed ad spend change directly contributes to the precision of the outcome. We can therefore determine whether a suggested ad spend change is sufficient for the experiment to be feasible.
One of the factors determining the standard error (and therefore, the precision) of our causal estimators is the amount of noise in the response variable. The noisier the data, the higher the standard error. On the other hand, for the models that we use, the standard error of the iROAS estimate is inversely proportional to the ad spend difference in the treatment group. That is, we can buy ourselves shorter confidence intervals (and a “higher precision”) by increasing the ad spend difference.
In practice, however, increasing precision is not always as easy as increasing spend. There might simply not be enough available inventory (such as ad impressions, clicks, or YouTube views) to increase spend. Further, there is the risk that the increased ad spend will be less productive due to diminishing returns (e.g., the first 100 keywords in a campaign will be more efficient than the next 100 keywords.)

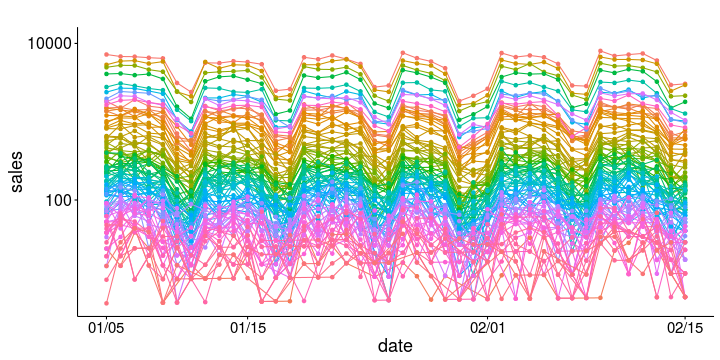
It is usually helpful to look at these response variables on a log scale. This really shows how similarly the geos behave, the only difference being their size.
The goal of the study was to estimate the incremental return in sales on an additional ad spend change. The 100 geos were randomly assigned to control and treatment groups, and a geo experiment test period was set up for February 16 – March 15, 2015, with the 6 previous weeks serving as the pre-period. During this test period, advertising spend was increased in the treatment group.

After the experiment was finished, the incremental return of ad spend was estimated to be $\beta_2 = 3.1$. The other parameters were $\beta_0 = 74$, and $\beta_1= 0.85$ with a residual standard deviation of 4.8. Since the pre-test period is 6 weeks long and the test period is 4 weeks long, a value of $\beta_1 = 0.85$ corresponds to a weekly trend of $(6/4) \times 0.85 = 1.27$, that is, on average each week the response volumes of the geos tend to increase by 27% (in the absence of any intervention). In practice, the focus of the team is however on the estimate of $\beta_2$, not to forget about the uncertainty around this estimate: the confidence interval half-width was estimated to be 0.27.
It is critical to apply appropriate diagnostics to the data and to the model fit before and after the test. In practice, anomalies often indicate issues with data reporting: untidy data and programming errors are a frequent source for headaches that are best addressed by developing tools that verify the integrity of the data and that check all model assumptions. For example, we have developed a few diagnostics tools of our own to catch unexpected features in the data such as outliers.
The model that we presented here is quite simple. It is then worth asking whether the model accounts for all of the factors that could influence the response. As usual, the honest answer is: probably not. One obvious omission is that the model presented ignores other possible predictors such as pricing and promotion information. And such information may not even be available. In the case of consumer packaged goods such as soft drinks or shampoo, for example, even manufacturers may not be aware of all the promotions going in each of the stores selling their products. Thanks to randomization, this omission will not bias our iROAS estimate. However, it will typically increase its variance.
It is a good idea to do a sensitivity analysis to check if there is any cause for concern. For example, one useful diagnostic to detect a single outlier geo is to look at the effect of each geo on the iROAS point estimate. In this leave-one-out analysis we repeat the analysis as many times as there are geos, each time dropping one geo from the analysis. By looking at a histogram of the estimates, we may see that dropping a particular geo may have a clear effect on the iROAS estimate.
Randomized experiments represent the gold standard for determining the causal effects of app or website design decisions on user behavior. We might be interested in comparing, for example, different subscription offers, different versions of terms and conditions, or different user interfaces. When it comes to online ads, there is also a fundamental need to estimate the return on investment. Observational data such as paid clicks, website visits, or sales can be stored and analyzed easily. However, it is generally not possible to determine the incremental impact of advertising by merely observing such data across time. One approach that Google has long used to obtain causal estimates of the impact of advertising is geo experiments.
What does it take to estimate the impact of online exposure on user behavior? Consider, for example, an A/B experiment, where one or the other version (A or B) of a web page is shown at random to a user. The analysis could then proceed with comparing the probabilities of clicking on a certain link on the page shown. The version of the web page that has a significantly higher estimated probability of click (click-through rate, or CTR) would be deemed the more effective one.
Similarly, we could test the effectiveness of a search ad compared to showing only organic search results. Whenever a user types in a specific search query, the system makes a split-second decision of whether or not to show a particular ad next to the organic results. Click-through rates can then be compared to determine the relative effectiveness of the presence of ads.
Traffic experiments like the ones above can randomize queries, but they cannot randomize users. The same user may be shown the ad whenever they perform the same search the second time. Traffic experiments, therefore, don't allow us to determine the longer term effect of the ad on the behavior of users.
We could approximate users by cookies. However, one user may have several devices (desktop, laptop, tablet, smartphone), each with its own cookie space. Moreover, cookies get deleted and regenerated frequently. Cookie churn increases the chances that a user may end up receiving a mixture of both the active treatment and the control treatment.
Even if we were able to keep a record of all searches and ad clicks and associate them with online conversions, we would still not be able to observe any long-term behavior. A conversion might happen days after the ad was seen, perhaps at a regular brick-and-mortar store. This makes it difficult to attribute the effect of an online ad on offline purchases.
It is important that we can measure the effect of these offline conversions as well. How can we connect an event of purchase to the event of perceiving the ad if the purchase does not happen immediately? And, from the perspective of the experiment set-up, how can we ensure that a user whom we assigned to the control group won't ever see the ad during the experiment?
Another possibility is to run a panel study, an experiment with a recruited set of users who allow us to analyze their web and app usage, and their purchase behavior. Panel studies make it possible to measure user behavior along with the exposure to ads and other online elements. However, meaningful insights require a representative panel or an analysis that corrects for the sampling bias that may be present. In addition, panel studies are expensive. Wouldn't it be great if we didn't require individual data to estimate an aggregate effect? Let's take a look at larger groups of individuals whose aggregate behavior we can measure.
A geo experiment is an experiment where the experimental units are defined by geographic regions. Such regions are often referred to as Generalized Market Areas (GMAs) or simply geos. They are non-overlapping geo-targetable regions. This means it is possible to specify exactly in which geos an ad campaign will be served – and to observe the ad spend and the response metric at the geo level. We can then form treatment and control groups by randomizing a set of geos.
Consider, as an example, the partition of the United States into 210 GMAs defined by Nielsen Media. The regions were originally formed based on television viewing behavior of their residents, clustering together “exclusive geographic area of counties in which the home market television stations hold a dominance of total hours viewed.” These geos can be targeted individually in Google AdWords. Here is an example of a randomized assignment:
In contrast to the US, France doesn't currently have an analogous set of geos. So we created a set of geos using our own clustering algorithms. The figure below shows an example of a set of geos partitioning mainland France into 29 GMAs:
Suppose that users in control regions are served ads with a total spend intensity of $C$ dollars per week, while users in treatment regions are served ads with a cost of $T = C + A$ dollars per week ($A > 0$). The key assumption in geo experiments is that users in each region contribute to sales only in their respective region. This assumption allows us to estimate the effect of the ad spend on sales. What makes geo experiments so simple and powerful is that they allow us to capture the full effects of advertising, including offline sales and conversions over longer periods of time (e.g., days or weeks).
Measuring the effectiveness of online ad campaigns
Estimating the causal effects of an advertising campaign, and the value of advertising in general, is what each of Google’s advertising clients would like to do for each of their products. There are many methods for estimating causal effects, and yet getting it right remains a challenging problem in practice.The quantity that we aim to estimate, in particular, is a specific type of return on investment where the investment is the cost of advertising. We often refer to this as the Return On Ad Spend (ROAS). Even more specifically, we are typically interested in the change in sales (or website visits, conversions, etc.) when we change the ad spend: the incremental ROAS, or iROAS. When response is expressed in terms of the same currency as the investment, iROAS is just a scalar. For example, an iROAS of 3 means that each extra dollar invested in advertising leads to 3 incremental dollars in revenue. Alternatively, when the response is the number of conversions, iROAS can be given in terms of number of conversions per additional unit of currency invested, say “1000 incremental conversions per 10,000 additional dollars spent.” In other words, iROAS is the slope of a curve of the response metric plotted against the underlying advertising spend.
Structure of a geo experiment
A typical geo experiment consists of two distinct time periods: pretest and test. During the pretest period, there are no differences in the ad campaign structure across geos. All geos operate at the same baseline level; the incremental difference between the control and treatment geos is zero in expectation. The pretest period is typically 4 to 8 weeks long.During the test period (which is typically 3 to 5 weeks long), geos in the treatment group are targeted with modified advertising campaigns. We know that this modification, by design, causes an incremental effect on ad spend. What we don't know is whether it also causes an incremental effect in the response metric. It is worth noting that modified campaigns may cause the ad spend to increase (e.g., by adding keywords or increasing bids in the AdWords auction) or decrease (e.g., by turning campaigns off). Either way, we typically expect the response metric to be affected in the same direction as spend. As a result, the iROAS is typically positive.
After the test period finishes, the campaigns in the treatment group are reset to their original configurations. This doesn't always mean their causal effects will cease instantly. Incremental offline sales, for example, may well be delayed by days or even weeks. When studying delayed metrics, we may therefore want to include in the analysis data from an additional cool-down period to capture delayed effects.
Designing a geo experiment: power analysis
As with any experiment, it is essential that a geo experiment is designed to have a high probability of being successful. This is what we mean when we estimate the power of the experiment: the probability of detecting an effect if an effect of a particular magnitude is truly present.Statistical power is traditionally given in terms of a probability function, but often a more intuitive way of describing power is by stating the expected precision of our estimates. We define this as the standard error of the estimate times the multiplier to obtain the bounds of a confidence interval. This could, for example, be stated as the “iROAS point estimate +/- 1.0 for a 95% confidence interval”. This is a quantity that is easily interpretable and summarizes nicely the statistical power of the experiment.
The expected precision of our inferences can be computed by simulating possible experimental outcomes. We also check that the false positive rate (i.e., the probability of obtaining a statistically significant result if the true iROAS is in fact zero) is acceptable, such as 5% or 10%. This power analysis is absolutely essential in the design phase as the amount of proposed ad spend change directly contributes to the precision of the outcome. We can therefore determine whether a suggested ad spend change is sufficient for the experiment to be feasible.
One of the factors determining the standard error (and therefore, the precision) of our causal estimators is the amount of noise in the response variable. The noisier the data, the higher the standard error. On the other hand, for the models that we use, the standard error of the iROAS estimate is inversely proportional to the ad spend difference in the treatment group. That is, we can buy ourselves shorter confidence intervals (and a “higher precision”) by increasing the ad spend difference.
In practice, however, increasing precision is not always as easy as increasing spend. There might simply not be enough available inventory (such as ad impressions, clicks, or YouTube views) to increase spend. Further, there is the risk that the increased ad spend will be less productive due to diminishing returns (e.g., the first 100 keywords in a campaign will be more efficient than the next 100 keywords.)
A model for assessing incremental return on ad spend
We are interested in estimating the iROAS, which for each geo is the ratio between the incremental (causal) revenue divided by the incremental change in expenditure in that geo. The incremental effect is defined as the difference between the expected potential outcome under treatment and the potential outcome under no treatment.
We estimate the causal treatment effect using linear regression (see for example [3], chapter 9). The model regresses the outcomes $y_{1,i}$ on the incremental change in ad spend $\delta_i$. We can however increase the precision of the estimates (and therefore the statistical power) by also including the pre-test response $y_{0,i}$ as a covariate:
For all control geos, we have $\delta_i = 0$ by design. For a treatment geo $i$, $\delta_i$ is the observed ad spend minus the counterfactual, that is, the ad spend that would have been observed in the absence of the treatment. This counterfactual is estimated using a linear regression model applied to control geos only (see [1] for details). If there was no previous ad expenditure (for this particular channel), the counterfactual estimate would simply be zero, and so i would be the observed spend in treatment geo $i$.
The modelled incremental response caused by the change in ad spend $\delta_i$ in geo $i$ is $\beta_2 \delta_i$. The model parameter $\beta_2$ is our main quantity of interest, the incremental ROAS. For example, $\beta_2 = 3.1$ would indicate that each unit of currency invested caused an extra 3.1 units of currency generated.
The term $\beta_1 y_{0,i}$ controls for seasonality and other factors common to all geos (e.g., a nationwide sales event), as it is plausible that the pretest and test periods experience a trend or a temporary increase that is unrelated to the effect we are measuring. The interpretation of the coefficient $\beta_1$, of course, depends on the length of the pretest and test periods.
The geos are invariably of different sizes and therefore the data show considerable heteroscedasticity. Since each geo can be thought of as being constructed from small individual contributions, we assume that the variance of a geo is proportional to its mean. This is a plausible assumption, since the variance of a sum of independent variables is equal to the sum of their individual variances. A variance stabilizing transformation (square root) is an option here to equalize the variances, but we prefer to work on the original scale (as opposed to square-root units), as this is more convenient and flexible; for example, the interpretation of the coefficients such as that of $\beta_2$ (iROAS) is straightforward. We have seen in practice that fitting the model using weighted regression with weights $1 / y_{0,i}$ (inverse of the sum of the response variable in the pretest period) controls heteroskedasticity. Without weighted regression we would obtain a biased estimate of the variance. Caution is needed, however, to use the weights: when the pre-test period volume of a geo are close to zero, the weights may be large (this usually reflects an issue with data reporting). A quick remedy is to combine the smallest geos to form a new larger geo.
The paper [1] gives more details on the model; the follow-up paper [2] describes an extension of the methodology to multi-period geo experiments.
We estimate the causal treatment effect using linear regression (see for example [3], chapter 9). The model regresses the outcomes $y_{1,i}$ on the incremental change in ad spend $\delta_i$. We can however increase the precision of the estimates (and therefore the statistical power) by also including the pre-test response $y_{0,i}$ as a covariate:
$y_{1,i} = \beta_0 + \beta_1 y_{0,i} + \beta_2 \delta_i + \epsilon_i$ for geo $i$
For all control geos, we have $\delta_i = 0$ by design. For a treatment geo $i$, $\delta_i$ is the observed ad spend minus the counterfactual, that is, the ad spend that would have been observed in the absence of the treatment. This counterfactual is estimated using a linear regression model applied to control geos only (see [1] for details). If there was no previous ad expenditure (for this particular channel), the counterfactual estimate would simply be zero, and so i would be the observed spend in treatment geo $i$.
The modelled incremental response caused by the change in ad spend $\delta_i$ in geo $i$ is $\beta_2 \delta_i$. The model parameter $\beta_2$ is our main quantity of interest, the incremental ROAS. For example, $\beta_2 = 3.1$ would indicate that each unit of currency invested caused an extra 3.1 units of currency generated.
The term $\beta_1 y_{0,i}$ controls for seasonality and other factors common to all geos (e.g., a nationwide sales event), as it is plausible that the pretest and test periods experience a trend or a temporary increase that is unrelated to the effect we are measuring. The interpretation of the coefficient $\beta_1$, of course, depends on the length of the pretest and test periods.
The geos are invariably of different sizes and therefore the data show considerable heteroscedasticity. Since each geo can be thought of as being constructed from small individual contributions, we assume that the variance of a geo is proportional to its mean. This is a plausible assumption, since the variance of a sum of independent variables is equal to the sum of their individual variances. A variance stabilizing transformation (square root) is an option here to equalize the variances, but we prefer to work on the original scale (as opposed to square-root units), as this is more convenient and flexible; for example, the interpretation of the coefficients such as that of $\beta_2$ (iROAS) is straightforward. We have seen in practice that fitting the model using weighted regression with weights $1 / y_{0,i}$ (inverse of the sum of the response variable in the pretest period) controls heteroskedasticity. Without weighted regression we would obtain a biased estimate of the variance. Caution is needed, however, to use the weights: when the pre-test period volume of a geo are close to zero, the weights may be large (this usually reflects an issue with data reporting). A quick remedy is to combine the smallest geos to form a new larger geo.
The paper [1] gives more details on the model; the follow-up paper [2] describes an extension of the methodology to multi-period geo experiments.
Example
Here is a set of daily time series data of sales by geo. As we will see further below, this period will form our pre-period for a geo experiment. There are 100 geos; the largest one has a volume that is 342 times that of the smallest one. Such differences in scale are not unusual. The time series shows significant weekly level seasonality, with the lowest volumes occurring during weekends.It is usually helpful to look at these response variables on a log scale. This really shows how similarly the geos behave, the only difference being their size.
The goal of the study was to estimate the incremental return in sales on an additional ad spend change. The 100 geos were randomly assigned to control and treatment groups, and a geo experiment test period was set up for February 16 – March 15, 2015, with the 6 previous weeks serving as the pre-period. During this test period, advertising spend was increased in the treatment group.
After the experiment was finished, the incremental return of ad spend was estimated to be $\beta_2 = 3.1$. The other parameters were $\beta_0 = 74$, and $\beta_1= 0.85$ with a residual standard deviation of 4.8. Since the pre-test period is 6 weeks long and the test period is 4 weeks long, a value of $\beta_1 = 0.85$ corresponds to a weekly trend of $(6/4) \times 0.85 = 1.27$, that is, on average each week the response volumes of the geos tend to increase by 27% (in the absence of any intervention). In practice, the focus of the team is however on the estimate of $\beta_2$, not to forget about the uncertainty around this estimate: the confidence interval half-width was estimated to be 0.27.
Caveats
Model
As with any statistical model, the model is designed to operate under certain assumptions. It is important that the technical assumptions of a linear regression model are satisfied: linearity, additivity, independence of errors, normality, and equal variance of errors (after taking into account the weighting). If the response data indeed consists of sums of small independent contributions (say, sales of products) that are grouped into geos, the differences between geos should be normally distributed. A more important assumption is that the relative volume of the geos will not be changing during the geo experiment.It is critical to apply appropriate diagnostics to the data and to the model fit before and after the test. In practice, anomalies often indicate issues with data reporting: untidy data and programming errors are a frequent source for headaches that are best addressed by developing tools that verify the integrity of the data and that check all model assumptions. For example, we have developed a few diagnostics tools of our own to catch unexpected features in the data such as outliers.
The model that we presented here is quite simple. It is then worth asking whether the model accounts for all of the factors that could influence the response. As usual, the honest answer is: probably not. One obvious omission is that the model presented ignores other possible predictors such as pricing and promotion information. And such information may not even be available. In the case of consumer packaged goods such as soft drinks or shampoo, for example, even manufacturers may not be aware of all the promotions going in each of the stores selling their products. Thanks to randomization, this omission will not bias our iROAS estimate. However, it will typically increase its variance.
Forming treatment groups
By randomizing, we aim to generate the treatment and control groups with comparable baseline characteristics. By complete randomization, we may well end up with groups that are not as balanced as we would prefer. By default, we use stratified randomization with each stratum containing geos of similar size. It may also be a good idea to consider forming strata by other characteristics such as geographical location.
Even stratified randomization may not be enough: the problem of balance may be especially accentuated when we have few geos to work with (for example, in small countries). Highly heterogeneous countries often have their own set of challenges. For example, the metropolitan areas of London and Paris dominate entire countries like the UK or France. This makes it virtually impossible to partition such countries into homogeneous, well-balanced groups.
For this reason, in these particular situations we need an algorithm that matches geos to form control and treatment groups that are predictive of each other, justifying a causal interpretation of the analysis.
Even stratified randomization may not be enough: the problem of balance may be especially accentuated when we have few geos to work with (for example, in small countries). Highly heterogeneous countries often have their own set of challenges. For example, the metropolitan areas of London and Paris dominate entire countries like the UK or France. This makes it virtually impossible to partition such countries into homogeneous, well-balanced groups.
For this reason, in these particular situations we need an algorithm that matches geos to form control and treatment groups that are predictive of each other, justifying a causal interpretation of the analysis.
Outliers
A particular nuisance is a geo that – for a known or unknown reason – experiences a shock (unexpected drop or surge) in the response variable during the test. For example, if a large geo in the control group suddenly experiences a heat wave, a geo experiment to measure the incremental sales of a particular ice cream brand might be affected, diluting the effect that we are aiming to measure. If the shock is balanced by another geo in the other group, this problem is fortunately mitigated (as it should be in a randomized experiment). Otherwise we will have to deal with the outlier geo(s) after the experiment. Hence we need to be aware of these problems and develop complementary methodologies to deal with them.It is a good idea to do a sensitivity analysis to check if there is any cause for concern. For example, one useful diagnostic to detect a single outlier geo is to look at the effect of each geo on the iROAS point estimate. In this leave-one-out analysis we repeat the analysis as many times as there are geos, each time dropping one geo from the analysis. By looking at a histogram of the estimates, we may see that dropping a particular geo may have a clear effect on the iROAS estimate.
Small market regions
Since the statistical power of this model depends on the number of geos, it is not obviously suitable for situations in which the number of geos is very small. In the U.S., for national level experiments we have no problem as we have over 210 geos. In Europe, use of this methodology may not be always advisable; as a rough rule of thumb, we prefer to apply this approach to experiments with 30, or more, geos. If this is not the case, alternative approaches relying on time-series models, such as CausalImpact, may be a better choice.What’s next?
We mentioned several challenges: ensuring the model is appropriate, lack of useful data, forming comparable treatment and control groups, dominant geos, outliers, and running experiments in small countries. For a data scientist, all this means more interesting and applicable research opportunities.References
- Jon Vaver and Jim Koehler, Measuring Ad Effectiveness Using Geo Experiments, 2011.
- Jon Vaver and Jim Koehler, Periodic Measurement of Advertising Effectiveness Using Multiple-Test-Period Geo Experiments, 2012.
- Andrew Gelman and Jennifer Hill, Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge, 2007.